/ Data Structure and Algorithms  

Leetcode 98. Validate Binary Search Tree

Question



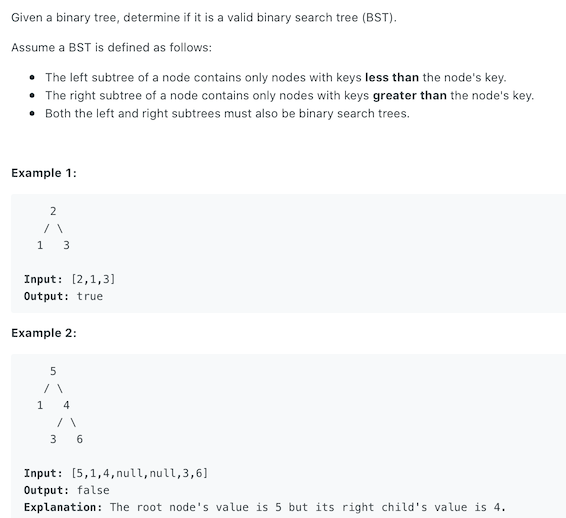
Given a tree, determine if the tree is a valid binary search tree. The binary search tree is defined as follows:
  • If the left subtree of any node is not empty, the values of all nodes on the left subtree are less than the value of its root node;
  • If the right subtree of any node is not empty, the value of all nodes on the right subtree is greater than the value of its root node;
  • The left and right subtrees of any node are also binary search trees;
  • There are no nodes with equal key values.

Similar Question

Solution - Recursion

The idea is that the left subtree is a legal binary search tree, the right subtree is a legal binary search tree, and the root node is larger than the largest number in the left subtree and smaller than the smallest number in the right subtree, then the current tree is a legal binary search tree

Solution - DFS

In previous solution, we are judging whether the root node is legal and found the largest number in the left subtree and the smallest number in the right subtree. The left and right subtrees determine whether the current root node is valid.

But normally, the root node comes first, it is reasonable to say that the root node could be any number rather than limited by the left and right subtrees. On the contrary, the root node determines the legal value range of the left and right subtree.

Therefore, we can do DFS from the root node, then calculate the value range that each node should take, and return false if the current node does not match.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
      10
    /    \
   5     15
  / \    /  
 3   6  7 

Consider 10's range
    10(-inf,+inf)

Consider 5's range
    10(-inf,+inf)
    /
5(-inf,10)

Consider 3's range
    10(-inf,+inf)
     /
   5(-inf,10)
    /
  3(-inf,5)  

Consider 6's range
    10(-inf,+inf)
     /
   5(-inf,10)
    /       \
3(-inf,5)  6(5,10)

Consider 15's range
    10(-inf,+inf)
    /          \
   5(-inf,10) 15(10,+inf）
    /       \
3(-inf,5)  6(5,10)  

Consider 7's range, if not match return false
        10(-inf,+inf)
         /           \
    5(-inf,10)     15(10,+inf）
  /       \           /
3(-inf,5)  6(5,10)  7（10,15）

It can be observed that the range of the left child is (left boundary of the parent node, the value of the parent node), and the range of the right child is (value of the parent node, the right boundary of the parent node).

We can pass Integer object, then null means negative infinity and positive infinity. Then use JAVA’s auto boxing and unboxing, the value comparison can be directly used inequality sign.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public boolean isValidBST(TreeNode root) {
    return isValid(root, null, null);
}

// every number has a valid range
// For node on left tree: (min of parent node, value of parent node)
// For node on right tree: (value of parent node, max of parent node)
private boolean isValid(TreeNode node, Integer min, Integer max) {
    if (node == null) {
        return true;
    }

    if (min != null && node.val <= min) {
        return false;
    }

    if (max != null && node.val >= max) {
        return false;
    }

    return isValid(node.left, min, node.val) && isValid(node.right, node.val, max);
}