Leetcode 89. Gray Code

Question

Generate n-bit Gray codes. The so-called Gray codes are two consecutive numbers with only one bit different.

Solution - Dynamic Programming

Use dynamic programming or recursive, that is, how to solve small problems and use it to solve large problems.

We assume that we have a solution of n = 2 and then consider how to get a solution of n = 3.

Solution of n = 2
00 - 0
10 - 2
11 - 3
01 - 1

If we add another bit, it is nothing more than adding 0 or 1 to the most significant bit. Consider adding 0 first. Since it is 0, the value has not changed.

Solution of n = 3, the most significant bit is 0
000 - 0
010 - 2
011 - 3
001 - 1

Then consider adding 1 and jsut putting 1 in the highest position based on the solution of n = 2?

Solution of n = 3
000 - 0
010 - 2
011 - 3
001 - 1  
------------- Below are added
100 - 4
110 - 6
111 - 7
101 - 5

It seems that it is not that simple. The fourth line 001 and the new fifth line 100 have 3 bits difference. So how to solve it?

Quite simply, the most significant bit of the new data in line 5 changed from 0 in the previous line 4 to 1, so don’t change the other bits, just pull the other bits in the 4th line, that is, 101.

Next, in order to make only one bit different between line 6 and line 5, because line 5 pulls the low bit of line 4, and line 4 and line 3 are only one bit different. So line 6 can take the low position of line 3. The other lines are the same, as shown below.

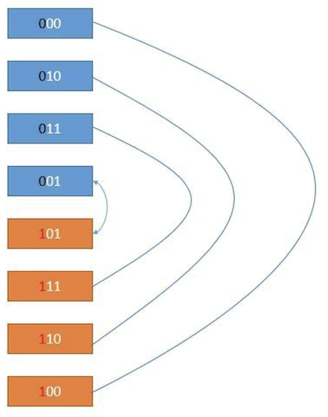
The blue part has the same value as all solutions with n = 2 because the most significant bit is 0. And the orange part adds 1 to the most significant bit, so if it is a value, add 4 to its corresponding value, which is 2², that is, 2^3-1, which is 1 << (n-1). So our algorithm can be solved by iteration.

So if we know the solution of n = 2, which is {0, 1, 3, 2}, then the solution of n = 3 is {0, 1, 3, 2, 2 + 4, 3 + 4, 1 + 4 , 0 + 4}, which is {0 1 3 2 6 7 5 4}. The previous solution is directly copied, and then each number plus 1 << (n-1) is added to the result in reverse order.

List<Integer> results = new ArrayList<>();
results.add(0);

for (int i = 0; i < n; i++) {
    int add = (int) Math.pow(2, i);

    for (int j = results.size() - 1; j >= 0; j--) {
        results.add(results.get(j) + add);
    }
}
        
return results;

Time complexity: 2ⁿ because there are such many results.

Space complexity: O (1).

Question

Similar Questions

Solution - Dynamic Programming