/ Data Structure and Algorithms  

Leetcode 86. Partition List

Question



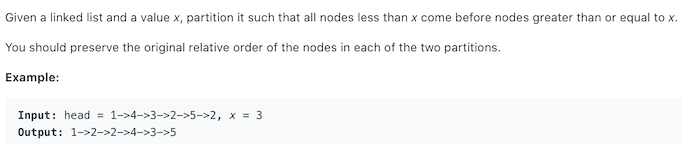
The question is essentially the partition of quick-sort. The linked list is divided into two parts, one part is less than the partition point x, and the other part is greater than or equal to the partition point x.

Solution

Looking at the quick-sort algorithm. In the quick-sort, we used two pointers for pivoting. One pointer indicates that the number before the pointer is less than the pivot point. The other pointer traverses the array.

1
2
3
4
5
6
7
8
9
10
11
12
13
1 4 3 2 5 2  x = 3
  ^   ^
  i   j

elements before i are less than pivot point 3
j means the current traverse point
when j point to a number that is less than pivot point, then we exchange the value at i and j, and move forward i

1 2 3 4 5 2  x = 3
    ^   ^
    i   j

Then just continue traversing

This question is just replacing array with linked list, and the question requires that the relative position of the numbers cannot be changed. So we must not use the exchange strategy, let alone the linked list exchange is more troublesome. In fact, we can just use the insert.

Similarly, a pointer is used to record the end of the linked list that is currently smaller than the pivot point, and another pointer is used to traverse the linked list. Each time we meet a number less than the pivot point, it is inserted into the end of the linked list and the end pointer is updated. We can use a dummy node to reduce the judgment of boundary conditions.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
// pivot node, first element that is >= x
ListNode pivot = head;

// dummy node
ListNode dummyHead = new ListNode(0);
dummyHead.next = head;

ListNode previousPivot = dummyHead;

// find the pivot value
while (pivot != null) {
    if (pivot.val >= x) {
        break;
    } else {
        previousPivot = pivot;
        pivot = pivot.next;
    }
}

// no value >= x or pivot is already the end, return list itself
// no need to modify
if (pivot == null || pivot.next == null) {
    return head;
}

// start from pivot, move all smaller node before pivot
ListNode current = pivot.next;
ListNode previous = pivot;

while (current != null) {
    // >= x, move to next
    if (current.val >= x) {
        previous = current;
        current = current.next;
    } else {
        final ListNode temp = current.next;

        previousPivot.next = current;
        current.next = pivot;
        previousPivot = current;

        previous.next = temp;
        current = temp;
    }
}

return dummyHead.next;

Time complexity: O(n).

Space complexity: O(1).