/ Data Structure and Algorithms  

Leetcode 64. Minimum Path Sum

Question



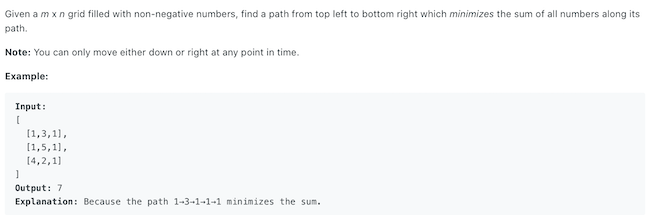
From top left to bottom right, find a path that minimize the sum along the path.

Similar Questions

Solution

Define a 2D array. Each element of the array represent the minimum sum starting from top left point to this point. For example, dp[i][j] = 5 means that starting from (0, 0) to (i, j), the minimum sum is 5.

The value on the first row, it is only reachable from its left point. And first column is only reachable from its up point.

For other points, the minimum sum is the sum of itself and minimum value of the point up it and left to it. Thus we have our dynamic programming formula: dp[i][j] = grid[i][j] + Math.min(dp[i - 1][j], dp[i][j - 1]). And we start to fill the dp array from second row.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// result grid
int[][] dp = new int[grid.length][grid[0].length];

dp[0][0] = grid[0][0];

// fill the first row, one reachable from its left point
for (int i = 1; i < grid[0].length; i++) {
    dp[0][i] = dp[0][i - 1] + grid[0][i];
}

// fill the first column, one reachable from its up point
for (int i = 1; i < grid.length; i++) {
    dp[i][0] = dp[i - 1][0] + grid[i][0];
}

// only one row or column
if (grid.length == 1 || grid[0].length == 1) {
    return dp[grid.length - 1][grid[0].length - 1];
}

// start from [1, 1], fill the result array
for (int i = 1; i < grid.length; i++) {
    for (int j = 1; j < grid[0].length; j++) {
        dp[i][j] = grid[i][j] + Math.min(dp[i - 1][j], dp[i][j - 1]);
    }
}

return dp[grid.length - 1][grid[0].length - 1];