/ Data Structure and Algorithms  

Leetcode 63. Unique Paths II

Question



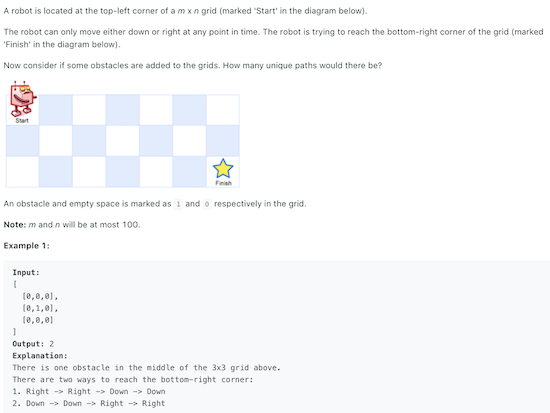
Similar to Question 62: Unique Paths. This time given a input array to mark obstacles.

Similar Questions

Solution

The solution is similar to Question 62: Unique Paths. Define a 2D array result. Each element of result represent the unique path starting from this point to bottom-right point.

The point on the last row and last column can only have 1 unique path (because we can only move right and down). However, if we traverse from the last to the first (e.g, from right to left or bottom to top), if there are any obstacle on the route, then the rest on the last row and last column is 0, as this route is blocked.

For other points, the number of unique paths is determined by unique path of the point below it and right to it. There are 3 situations:

  1. If both bottom and right point is obstacle or the position itself is obstacle, set to 0
  2. If only one of bottom and right point is obstacle, set to right or bottom
  3. Otherwise, result[i][j] = result[i + 1][j] + result[i][j + 1].

Finally we just need to get the value of result[0][0]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
// get number of columns and rows
int columns = obstacleGrid[0].length;
int rows = obstacleGrid.length;

// result array
int[][] result = new int[rows][columns];

// check if the bottom-right point itself is obstable or not
result[rows - 1][columns - 1] = obstacleGrid[rows - 1][columns - 1] == 1 ? 0 : 1;

// to mark if encounter any obstacle on last row
int obstacle = 0;

// fill right most column and last row with 1 or 0
for (int i = columns - 1; i >= 0; i--) {
    if (obstacleGrid[rows - 1][i] == 1) {
        obstacle = -1;
    }
    
    result[rows - 1][i] = 1 + obstacle;
}

// to mark if encounter any obstacle on last column
obstacle = 0;
for (int i = rows - 1; i >= 0; i--) {
    if (obstacleGrid[i][columns - 1] == 1) {
        obstacle = -1;
    }

    result[i][columns - 1] = 1 + obstacle;
}

// start from second last row and column
for (int i = rows - 2; i >= 0; i--) {
    for (int j = columns - 2; j >= 0; j--) {
        // both right or below point is obstacle or the point itself is obstacle
        if ((obstacleGrid[i][j + 1] == 1 && obstacleGrid[i + 1][j] == 1) || obstacleGrid[i][j] == 1) {
            result[i][j] = 0;
        // the point below is obstacle
        } else if (obstacleGrid[i][j + 1] == 1) {
            result[i][j] = result[i + 1][j];
        // the point at right is obstacle
        } else if (obstacleGrid[i + 1][j] == 1) {
            result[i][j] = result[i][j + 1];
        } else {
            result[i][j] = result[i][j + 1] + result[i + 1][j];
        }
    }
}

return result[0][0];