/ Data Structure and Algorithms  

Leetcode 60. Permutation Sequence

Question



Given an n, not to output its full permutation, but to arrange all combinations from small to large, and output the kth.

Similar Questions

Solution

Take n = 4 as an example. Because it is arranged from small to large, the highest digit must be from 1 to 4. Then it can be seen as a group, we only need to look for the group number to know what the highest digit is. And the number of each group is the (n-1)!.



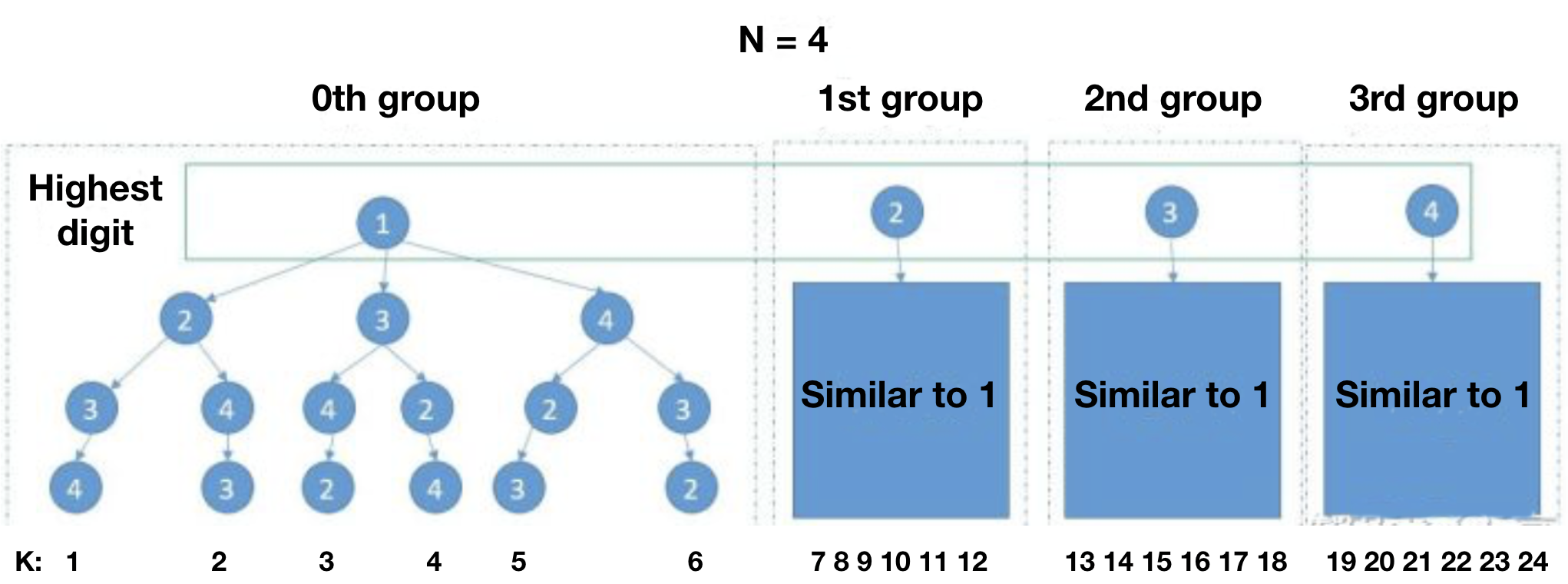
When calculating the group number, 1 to 5 divided by 6 is 0, 6 divided by 6 is 1, and 6 belongs to group 0, so we need to subtract 1 from k. By doing this, the division results are all 0.

1
2
int perGroupNum = factorial(n - 1); 
int groupNum = (k - 1) / perGroupNum;

Of course, there is also the question of what k is next time. Divide the group number, and the remainder is the next k. Because k is counted from 1, if k is exactly equal to a multiple of perGroupNum, the remainder obtained at this time is 0. In fact, since we subtract 1 when we ask for groupNum, k should be updated to perGroupNum at this time.

1
2
k = k % perGroupNum; 
k = k == 0 ? perGroupNum : k;

For example, if k = 6, then groupNum = (k-1) / 6 = 0, k % perGroupNum = 6% 6 = 0, and the next k can be seen from the above figure, it is obviously perGroupNum, which is still 6.

After determining that the highest digit belongs to group 0, then the next is the same as the above process. The only difference is that the highest digit is 2 3 4 and there is no 1. How to get the highest digit of groupNum needs to be considered.

We can use a list to save 1 to n from small to large, and remove one digit each time, so that we can get the number corresponding to groupNum.

Combine then together, we get the following solution.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
// record `n!`, keep it here to speed up
private Map<Integer, Integer> factorialTable = new HashMap<>();

public String getPermutation(int n, int k) {
    List<Integer> nums = new ArrayList<>();

    // put 1 - n to a list
    for (int i = 1; i <= n; i++) {
        nums.add(i);
    }

    return getResult(nums, n, k);
}

// nums initially is '1,2,3,4,5,....n'
private String getResult(List<Integer> nums, int n, int k) {
    StringBuilder stringBuilder = new StringBuilder();

    while (n > 1) {
        // permutation starting with the same number is a group
        // how many number in each group? n!
        // e.g. if n = 3, each group has 2 numbers
        int numPerGroup = factorial(n - 1);
        // which group is our target number in
        int groupNum = (k - 1) / numPerGroup;

        stringBuilder.append(nums.get(groupNum));

        k = k % numPerGroup;
        k = k == 0 ? numPerGroup : k;

        nums.remove(groupNum);
        n--;
    }

    stringBuilder.append(nums.get(0));

    return stringBuilder.toString();
}

private int factorial(int n) {
    if (n == 1) {
        factorialTable.put(n, 1);
        return 1;
    } else {
        if (factorialTable.containsKey(n - 1)) {
            int result = n * factorialTable.get(n - 1);
            factorialTable.put(n, result);
            return result;
        } else {
            int result = n * factorial(n - 1);
            factorialTable.put(n, result);
            return result;
        }
    }
}