/ Data Structure and Algorithms  

Leetcode 47. Permutations II

Question



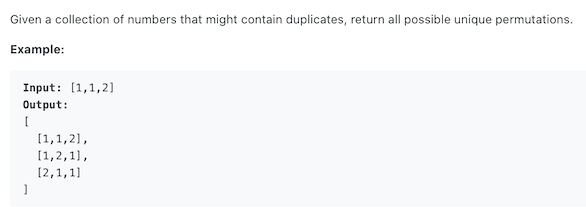
Similar to 46. Permutations, the difference is that there will be duplicates in the input, so using the previous algorithm will produce duplicate sequences. For example, [1 1], using the previous algorithm, the result must be [[1 1], [1 1]]. In other words, a repeated sequence is generated. But we can modify the solution to the previous question to solve this problem.

Similar Questions

Solution

Look at the previous solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public List<List<Integer>> permute(int[] nums) {
    List<List<Integer>> result = new ArrayList<>();

    backtrack(result, new ArrayList<>(), nums);

    return result;
}

private void backtrack(List<List<Integer>> result, List<Integer> tempList, int[] nums) {
    // find a solution, add to result
    if (tempList.size() == nums.length) {
        result.add(new ArrayList<>(tempList));
    }

    for (int num : nums) {
        // if already have the number, skip
        if (tempList.contains(num)) {
            continue;
        }

        tempList.add(num);

        // continue adding next one
        backtrack(result, tempList, nums);

        // remove the last added one
        tempList.remove(tempList.size() - 1);
    }
}

The first thing to resolve is these lines of code

1
2
3
if (tempList.contains(num)) {
    continue;
}

There are no duplicate elements before, so we can directly determine whether there is a current element in tempList and skip it if there is one. But here, because there are duplicate elements, this method is obviously not possible.

Put another way, we can use another list to save the index of the elements already in the current tempList, and then decide if index already exist when adding new elements.

The second problem is that when we have duplicate elements, the generated result may contain same list, which is unnecessary.

The solution is to sort the array first, and then determine whether the previously added element is equal to the current element. If they are equal, skip it and continue to the next element.

Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
public List<List<Integer>> permuteUnique(int[] nums) {
    List<List<Integer>> result = new ArrayList<>();

    Arrays.sort(nums);

    backtrack(nums, new ArrayList<>(), new ArrayList<>(), result);

    return result;
}

private void backtrack(int[] nums, List<Integer> tempList, List<Integer> indexList, List<List<Integer>> result) {
    if (tempList.size() == nums.length) {
        result.add(new ArrayList<>(tempList));
    }

    for (int i = 0; i < nums.length; i++) {
        // already have the elements added
        // solve the first problem
        if (indexList.contains(i)) {
            continue;
        }

        // remove duplicates
        // solve the second problem
        if (i > 0 && !indexList.contains(i - 1) && nums[i - 1] == nums[i]) {
            continue;
        }

        indexList.add(i);
        tempList.add(nums[i]);

        backtrack(nums, tempList, indexList, result);

        indexList.remove(indexList.size() - 1);
        tempList.remove(tempList.size() - 1);
    }
}

To solve the second problem !indexList.contains(i - 1) is very important because the above indexList.contains(i) code will make some elements skipped and not added to the tempList, so we have to determine whether nums[i-1] is the skipped element, if indexList.contains(i) returns true, even if nums[i-1] == nums[i] cannot skip the current element. Because the previous element nums[i-1] was not added to the tempList.