/ Data Structure and Algorithms  

Leetcode 34. Find First and Last Position of Element in Sorted Array

Question



Find the first and last location of target value in a sorted array. Algorithm need to run in O(logn).

Similar Questions

Solution 1 Linear Scan

Note that the array is sort. So we can make use of that. First scan from left to right. Once target value is found, stop scanning and record the index. Then scan from right to left, and record the index of first occurance of target value.

If target value is not found when scanning from left to right, then we can directly return [-1. -1] as there is no target value in the array.

This algorithm is easy enough. However, time complexity is O(n), so it is not what we really want.

Solution referenced from here: https://leetcode.wang/leetCode-34-Find-First-and-Last-Position-of-Element-in-Sorted-Array.html

As we are targeting O(logn), binary search is a good candidate.

In a normal binary search, our algorith ends as soon as we find the target value. It may not be the leftmost target value. Like in the following case (pic taken from: ):



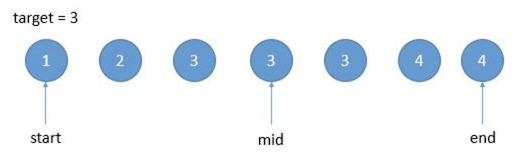
In this case we need to keep looking for the leftmost target value. So once we found the target value, insted of return, we make end = mid - 1 to keep searching. Eventually, the start will stop at the leftmost target value.

We can do the same to find the rightmost target value. The end will stop at the rightmost target value

Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
int start = 0;
int end = nums.length - 1;

// array to record the result
int[] result = new int[]{-1, -1};

if (nums.length == 0) {
    return result;
}

// first, try to find target, and keep search left part
// when this loop exit, start must point to the leftmost target, or target not exist
while (start <= end) {
    int mid = (start + end) / 2;

    // find target, keep search left
    if (nums[mid] == target) {
        end = mid - 1;
    } else if (nums[mid] > target) {
        end = mid - 1;
    } else {
        start = mid + 1;
    }
}

if (start == nums.length || nums[start] != target) {
    // didn't find target
    return result;
} else {
    result[0] = start;
}

// search rightmost target
start = 0;
end = nums.length - 1;

while (start <= end) {
    int mid = (start + end) / 2;

    // find target, keep search right part
    if (nums[mid] == target) {
        start = mid + 1;
    } else if (nums[mid] > target) {
        end = mid - 1;
    } else {
        start = mid + 1;
    }
}

// we already know that target exist
// end will convergence to target
result[1] = end;

return result;

Time complexity O(logn), and space complexity O(1).