/ Data Structure and Algorithms  

Leetcode 221. Maximal Square

Question



The output the maximum square area of 1 within a given array.

Similar Questions

Solution

Use dp[i][j] to denote the maximum length of the square with matrix[i][j] as the lower right corner. Then the recursion formula is as follows:

  • The initial condition is that dp[i][j] = matrix[i][j]-'0' in the first row and first column, which means that dp[i][j] is either 0 or 1.

  • Then there is recursion.
    dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1
    That is, select the minimum value among the three points on the left, top, and upper left corner of the current point, and then add 1.

First of all, it must be clear that dp[i][j] represents the maximum length of the square with matrix[i][j] as the lower right corner.

Then we expand from the current point to the left and upward, we can refer to the figure below



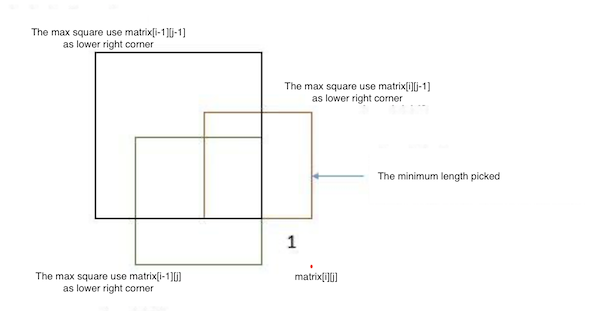
How much can we expand to the left? For dp[i][j-1] and dp[i-1][j-1], select the smaller one to the left and upper left corner of the current point. That is, the largest square on its left and the largest square on its upper left corner, pick the smaller side length.

How much can we expand to up? dp[i-1][j] and dp[i-1][j-1], choose the smaller one above the current point and the upper left corner. That is, the largest square on the upper side and the largest square on the upper left corner, pick the smaller side length.

Then choose the smaller one from expand the left and expand the up. Finally, add 1 to get the final side length.

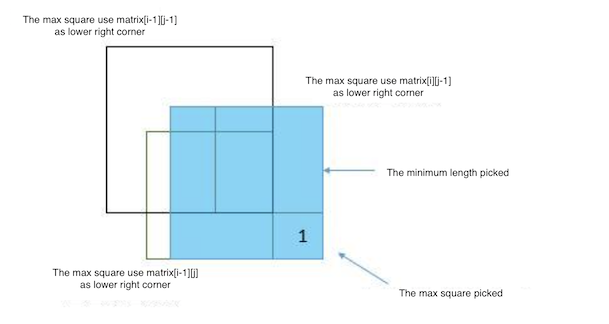
Finally it is actually the smallest side length from the three squares.



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public int maximalSquare(char[][] matrix) {
    int row = matrix.length;

    if (row == 0) {
        return 0;
    }

    int col = matrix[0].length;

    // additional row and col to avoid judge first row and col
    int[][] dp = new int[row + 1][col + 1];

    int result = 0;

    for (int i = 1; i <= row; i++) {
        for (int j = 1; j <= col; j++) {
            if (matrix[i - 1][j - 1] == '0') {
                dp[i][j] = 0;
            } else {
                // dp[i][j] = Min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1]) + 1
                dp[i][j] = Math.min(dp[i - 1][j], Math.min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;

                result = Math.max(dp[i][j], result);
            }
        }
    }

    return result * result;
}