Leetcode 220. Contains Duplicate III

Question

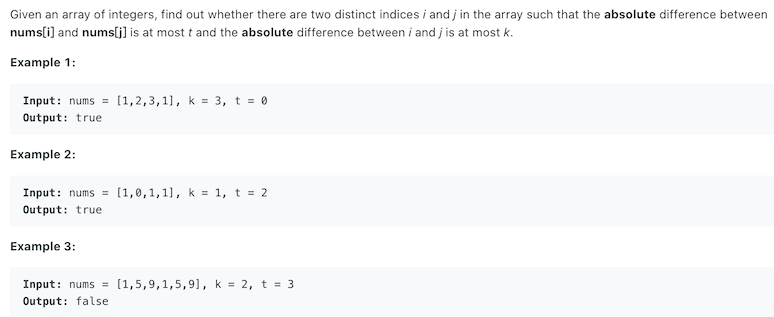
Given an array, determine whether there are two numbers, the difference between the index does not exceed k, and the difference between the two numbers does not exceed t.

Solution - Brute Force

Use 2 for loop to determine whether the current number and the index are within a distance of k and the difference between the values does not exceed t

public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
    int n = nums.length;

    for (int i = 0; i < n; i++) {
        for (int j = 1; j <= k; j++) {
            if (i + j >= n) {
                break;
            }
            if (Math.abs(nums[i] - nums[i + j]) <= t) {
                return true;
            }
        }
    }
    return false;
}

The above does not seem to have any problem, but for some subtraction, overflow may occur. For example, Integer.MAX_VALUE - (-2) will overflow. Some overflow may cause problems in our final result. The most direct solution is to force the int to be converted to long for calculation.

public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
    int n = nums.length;
    for (int i = 0; i < n; i++) {
        for (int j = 1; j <= k; j++) {
            if (i + j >= n) {
                break;
            }
            if (Math.abs((long) nums[i] - nums[i + j]) <= t) {
                return true;
            }
        }
    }
    return false;
}

Solution - TreeSet

We can make use of the TreeSet data structure.

There is a method public E ceiling(E e) that returns the smallest element in the TreeSet that is greater than or equal to e, or null if there is no element greater than or equal to e.

There is also a corresponding method, public E floor(E e), which returns the largest element in the TreeSet that is less than or equal to e, or returns null if there is no element less than or equal to e.

The time complexity of both methods is O(log(n)).

We can use a sliding window. For example:

1
2
3

k = 3, t = 2, store the 3 numbbers in the windown in TreeSet. Let's consider x
2 6 3 x 5
^   ^

Now we go to find whether there is an element of x-t ~ x + t in the window.

If we call ceilling(x - t) and return c, c is the smallest number in the window that is greater than or equal to x - t. As long as c is not greater than x + t, then c must be what we are looking for. Otherwise, we continues to move the window to the right.

public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
    TreeSet<Long> numberSet = new TreeSet<>();

    // construct a sliding window
    // window contains `k` elements
    for (int i = 0; i < nums.length; i++) {
        // need to remove item from the window
        if (i > k) {
            numberSet.remove((long)nums[i - k - 1]);
        }

        // if current element is nums[i], try to find the min element in the window >= nums[i] - t
        // if the min element <= nums[i] + t, then we found the number
        Long temp = numberSet.ceiling((long)nums[i] - t);

        if (temp != null && temp <= (long)nums[i] + t) {
            return true;
        }

        numberSet.add((long)nums[i]);
    }

    return false;
}

Question

Similar Questions

Solution - Brute Force

Solution - TreeSet