/ Data Structure and Algorithms  

Leetcode 19. Remove Nth Node From End of List

Question



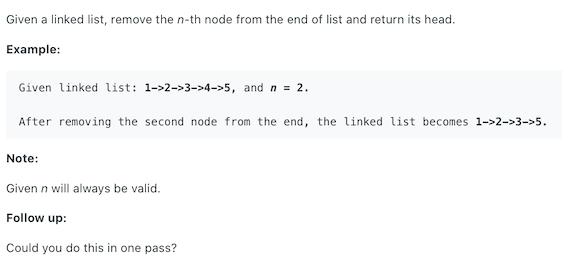
Given a linked list, delete the nth node from the end.

Solution - 2 Pass

Deleting a node is nothing more than traversing the linked list and find the node in front of the node to be deleted. However because it is a linked list, we don’t know its length. So we have to traverse the list first to get its length, then subtract n from the length to find the position of the node to be deleted.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public ListNode removeNthFromEnd(ListNode head, int n) {
    int length = 0;
    ListNode node = head;

    while (node != null) {
        length++;
        node = node.next;
    }

    // only 1 node in the list
    if (length == 1) {
        return null;
    }

    // index to remove, start from 0
    int indexToRemove = length - n;

    node = head;
    // move to the previous node
    for (int i = 0; i < indexToRemove - 1; i++) {
        node = node.next;
    }

    node.next = node.next.next;

    return head;
}

Time complexity: assuming the length of the linked list is L, then the first loop is L times, and the second loop is L-n times, for a total of 2L-n times, so the time complexity is O (L).

Space complexity: O (1).

Solution - 1 Pass

So how can we traverse the list only once?

We set two pointers, let the first pointer traverse forward n steps, and then let them both traverse at the same time. In this case, when the first pointer reaches the end, the second pointer is n steps from the head. So the position of the second pointer is exactly the nth node from the head.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public  ListNode removeNthFromEnd(ListNode head, int n) {
    ListNode dummyNode = new ListNode(0);
    dummyNode.next = head;

    ListNode pointer1 = dummyNode;
    ListNode pointer2 = dummyNode;

    // move first pointer ahead n steps
    for (int i = 0; i <= n; i++) {
        pointer1 = pointer1.next;
    }

    while (pointer1 != null) {
        pointer1 = pointer1.next;
        pointer2 = pointer2.next;
    }

    // now pointer2 is the node before the node to be delete
    pointer2.next = pointer2.next.next;

    return dummyNode.next;
}

Time complexity:

The first pointer goes from 0 to n, then “the first pointer goes from n to the end” and “the second pointer goes from 0 to the position of the n-th node down” simultaneously.

The previous solution is nothing more than going from 0 to the end, and then going from 0 to the position of the n-th node.

So in fact, the number of times their statements are executed is the same. The position of the n-th node from 0 to the penultimate point is traversed twice, so the total is 2L-n times. It’s just that this solution combines the two loops of solution one, so that the second pointer seems to traverse by the way, the idea is very nice.

So in essence, they are actually the same, and the time complexity is still O(n).

Space complexity: O (1).