/ Data Structure and Algorithms  

Leetcode 166. Fraction to Recurring Decimal

Question



Do arithmetic division, if it is a cyclic decimal, the part of the loop should be enclosed in parentheses.

Solution

In simple words, this question is actually a simulation of our division process.

First, let ’s talk about what process we want to simulate, taking 20/11 as an example.

The quotient obtained for the first time is the integer part, denoted as integer. We can directly use division between two ints.

1
integer = 20 / 11 = 1

Then let’s recall the process of division.

As shown in the figure below, the quotient is 1, and the remainder is 9. To get the remainder in the program, we can use numerator - quotient * denominator.

1
remainder = 20 - 1 * 11 = 9


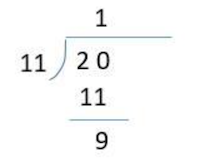
Next we multiply the remainder by 10 as the new numerator, and continue to use 11 as the denominator. Then get the quotient and the new remainder.

So calculate 90/11.



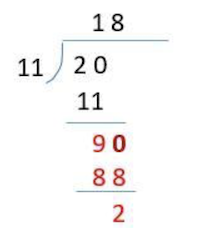
Then repeat the above process, multiply the remainder by 10 as the new numerator, and continue to use 11 as the denominator. Then get the quotient and the new remainder.

So calculate 20/11.



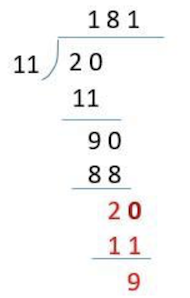
Then repeat the above process again, multiply the remainder by 10 as the new numerator, and continue to use 11 as the denominator. Then get the quotient and the new remainder.

So calculate 90/11.



So when does it end?

  1. The remainder is 0, indicating that there is no cyclic decimal.
  2. At first, I felt that as long as there are repeated quotient (not considering the integer part number, which is the first 1 in the above example), it can be considered that there is a cyclic decimal.

In the above example, 8 appears for the second time, so it will not be calculated further. The decimal part of the loop is the position that repeats from the previous appearance of current number to the previous position, which is 81. So the final result is 1.(81).

However there is a counterexample as below:



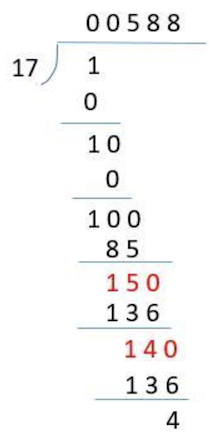
Although there are repeated 8s, the end result is not 8 cycles. Obviously next time it will be 40/17, and quotient is 2. The reason is that the numerator corresponding to the two quotients 8 are not the same. The first is 150 and the second is 140.

Therefore, in order to judge whether there is a cyclic decimal, we should not judge whether there is a repeated quotient, but rather whether there is a repeated dividend.

Therefore, in order to determine whether there is a cyclic decimal, we should not judge whether there is a repeated quotient, but rather whether there is a repeated numerator.

To record quotient, we will record the integer part and the decimal part separately. Because the decimal part has to accumulate records, For example, the first quotient is 1, and the second quotient is 2. We can multiply the previous quotient by 10 and add the new quotient. That is, 1 * 10 + 2 = 12, when the third quotient 5 comes, it is 12 * 10 + 5 = 125.

But for the above example 1/17, the first quotient is 0, and the second quotient is 5. If the above recording method is used, 5 is recorded instead of 05. In addition, if there are too many parts of the quotient, overflow will occur, so we need to record the quotient with String, and a new quotient can be added to the String each time.

Another question is how to determine whether there are duplicate quotients?

Quite simply, using a HashMap, key records the numerator that have occurred, and value records where the quotient appears, so that when repeated dividends occur, we can immediately know what the fractional part of the loop is by value.

The last question, we only considered the example of positive numbers divided by positive numbers. What about positive numbers divided by negative numbers or negative numbers divided by negative numbers? Just like we did on paper, first determine the sign of the quotient, and then convert both the numerator and the denominator to positive numbers.

The above operation will cause a problem. In java, for int type, the minimum value of negative number is -2147483648, the maximum value of positive number is 2147483647, and -2147483648 cannot be converted into a positive number.

The problem of overflow is actually not the key to this problem, so we can simply use the long data type to store the number.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
public String fractionToDecimal(int numerator, int denominator) {
    long num = numerator;
    long den = denominator;

    String sign = "";

    // first determine the sign
    if ((num > 0 && den < 0) || (num < 0 && den > 0)) {
        sign = "-";
    }

    // make num and den positive
    num = Math.abs(num);
    den = Math.abs(den);

    // determine the digit before decimal point
    long integer = num / den;

    // use a map to record encountered num and it's location
    Map<Long, Integer> map = new HashMap<>();

    // location of index after decimal point
    int index = 0;

    // use a string to record all digits after decimal point
    StringBuilder decimal = new StringBuilder();

    // mark the location of starting point of repeating
    int repeatingIndex = -1;

    // get the remaining
    num = num - integer * den;

    // enter while loop
    // condition to exit: remaining is 0 or find repeating
    while (num != 0) {
        // remaining * 10
        num = num * 10;

        // find if we have already encountered this 'num' before
        if (map.containsKey(num)) {
            repeatingIndex = map.get(num);
            break;
        }

        // put num to map
        map.put(num, index);

        // calculate new digit
        long temp = num / den;

        decimal.append(temp);

        // update num
        num = num - temp * den;

        // increase index
        index++;
    }

    // see if there is repeating
    if (repeatingIndex != -1) {
        return sign + integer + "." + decimal.substring(0, repeatingIndex) + "(" + decimal.substring(repeatingIndex) + ")";
    } else {
        if (decimal.length() == 0) {
            return sign + integer;
        } else {
            return sign + integer + "." + decimal;
        }
    }
}