/ Data Structure and Algorithms  

Leetcode 153. Find Minimum in Rotated Sorted Array

Question



Given a rotated sorted array, find the smallest number.

Similar Questions

Solution

To find the minimum value, we can certainly traverse the whole array. However here is an ordered array, so we can use the dichotomy method to find, the dichotomy method should ensure that after each comparison, half of the elements are removed.

Here we compare the midpoint and the end point. So do we compare the midpoint and the start point, or the midpoint and the end point? Let’s analyze it.

Compare mid and start

mid > start: The minimum value is in the left half



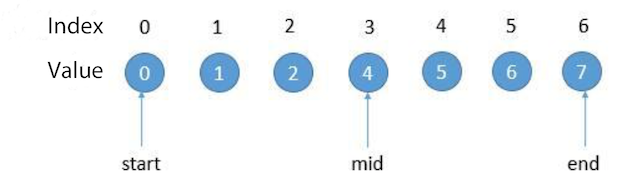
mid < start: the minimum value is in the left half



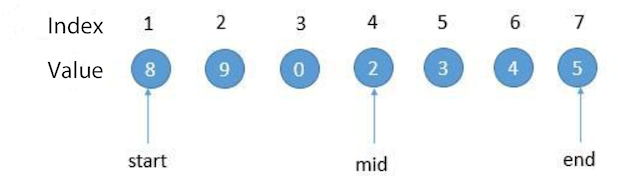
Whether mid is greater or less than start, the minimum value is always in the left half. So mid and start comparison is not desirable.

Compare mid and end

mid < end: The minimum value is in the left half





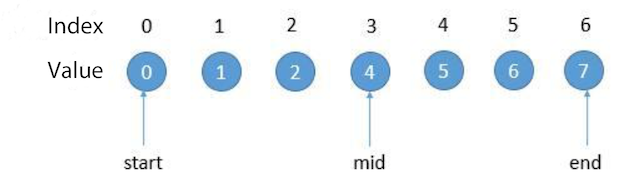
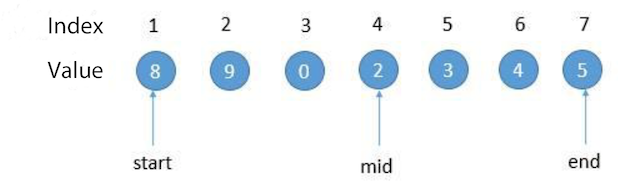
mid > end: The minimum value is in the right half



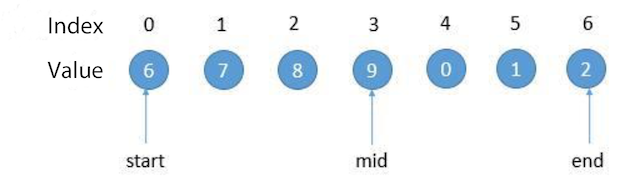
So we only need to compare mid and end, mid < end discards the right half (update end = mid), mid > end discards the left half (update start = mid). It can be finished until end is equal to start.

But there will be a problem for the following example, we will get an endless loop:



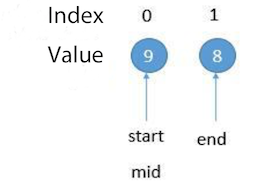
The problem is that when there are two elements left, mid = (start + end) / 2, and mid equals start. In the example above, mid > end, update start = mid, the position of start will not change. Then the value of mid will not change next time, it will endlessly. Therefore, we need to update start = mid + 1, and also make start point to the minimum value.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public int findMin(int[] nums) {
    // use binary search
    // start, mid, end
    // compare mid and start
    // if mid < end, means right half is sorted, min value must be in left half
    // if mid > end, means array must pivot at some value in the right half, thus min in the right half
    int start = 0;
    int end = nums.length - 1;

    while (start < end) {
        int mid = (start + end) / 2;

        if (nums[mid] > nums[end]) {
            start = mid + 1;
        } else {
            end = mid;
        }
    }

    return nums[start];
}