/ Data Structure and Algorithms  

Leetcode 142. Linked List Cycle II

Question



Given a linked list, determine the entry point of the loop. The entry point is essentially the intersection point of the line and the circle.

Similar Questions

Solution - HashSet

Traverse the linked list, and save the traversed nodes with HashSet. If we encounter the previous node during the traversal, it means that this node is the entry point we want to find. If it reaches null, there is no loop.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public ListNode detectCycle(ListNode head) {
    Set<ListNode> nodes = new HashSet<>();

    while (head != null) {
        nodes.add(head);

        head = head.next;

        if (nodes.contains(head)) {
            return head;
        }
    }

    return null;
}

Solution - Two Pointers

Two pointers is one of the most commonly used method when solving linked list problems.

The principle of fast and slow pointers is easy to understand. Imagine a round track where two people are running. If one person runs fast and one person runs slowly, then no matter where they start from, the two will definitely meet during the run.
So here we use two pointers fast and slow. Fast takes two steps at a time, and slow takes one step at a time. If fast reaches null, there is no ring. If fast and slow meet, there is a loop.

But for this problem, we need to find the entry point, and the point where the fast and slow pointers meet may not be the entry point, but a certain point in the loop, so some mathematical derivation is needed here. Referenced from: https://leetcode.com/problems/linked-list-cycle-ii/discuss/44793/O(n)-solution-by-using-two-pointers-without-change-anything



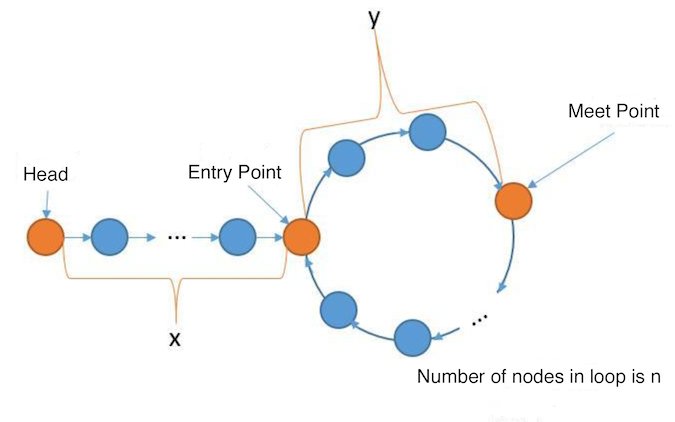
The distance from the head to the entry point is set to x, the distance from the entry point to the meeting point is set to y, and the length of the loop is set to n.

Assuming the distance traveled by the slow pointer is t, then the fast pointer must travel twice the distance of the slow pointer, which is 2t.

The slow pointer starts from the head and walks the distance of x to reach the entry point, and then possibly walks k1 circles, then returns to the entry point again, and then walks the distance of y to reach the meeting point and meet the fast pointer.

1
t = x + k1 * n + y

The same applies to the fast pointer. The fast pointer starts from the head and walks a distance of x to reach the entry point, and then possibly walks k2 circle, then returns to the entry point again, and then walks a distance of y to reach the meeting point and meet the slow pointer.

1
2t = x + k2 * n + y

Take the difference by the two equations above, you can get

1
t = (k2 - k1) * n

Let k = k2-k1, then t = k * n.

Substitute t = k * n into the first expression t = x + k1 * n + y.

1
k * n = x + k1 * n + y

Shift term, x = (k-k1) * n-y

Take a combination of n and y, get:

1
x = (k-k1-1) * n + (n-y)

The left part of the equation means: reach the entry point from head.

The right part of the equation means: n-y is the distance from the meeting point to the entry point, (k-k1-1) * n is to turn (k-k1-1) circle.

Combining left and right part: walking from the meeting point to the entry point, then turning (k-k1-1) circle and returning to the entry point again is exactly the same time from head to the entry point.

So for the code, we only need the meet pointer to start from the meeting point, and let the head pointer also start. The position where the head pointer meets the meet pointer is the entry point.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public ListNode detectCycle(ListNode head) {
    ListNode slow = head;
    ListNode fast = head;
    ListNode meet = null;

    while (fast != null) {
        // no loop
        if (fast.next == null) {
            return null;
        }
    }

    // move forward slow and fast
    slow = slow.next;
    fast = fast.next.next;

    // reach the meet point
    if (fast == slow) {
        meet = fast;

        // start move forward head, until meet point
        while (head != meet) {
            head = head.next;
            meet = meet.next;
        }

        return head;
    }

    return null;
}