Leetcode 130. Surrounded Regions | Nick Li

Question

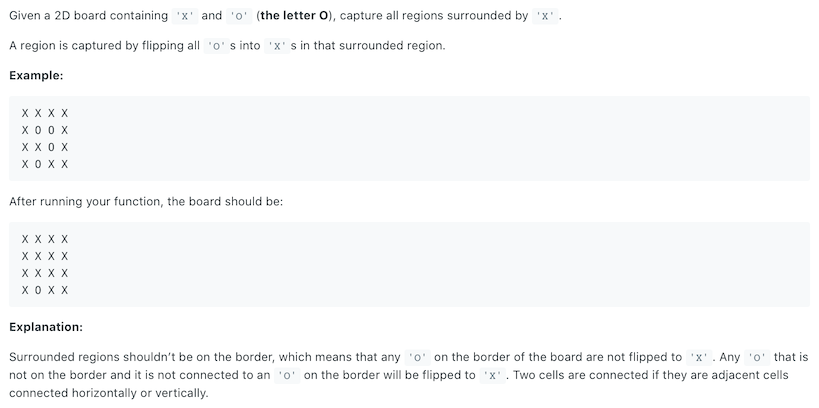
It’s a little bit like Go, turning the O enclosed by X into X, and the O at the boundary will not be enclosed. If O and O on the boundary are connected, then these O are counted as unenclosed, as in the example below.

X X X X X
O O O X X
X X X O X
X O X X X

The example above only needs to change one O.

X X X X X
O O O X X
X X X X X
X O X X X

Similar Question

• Medium - 200. Number of Islands

Solution - DFS

Consider adjacent O as a connected graph, and then start DFS from each O.

If O does not reach the boundary after the traversal is completed, we change the current O to X (meaning this O is not connected to a O at the boundary, hence enclosed by X).

If the boundary O is reached during the traversal, DFS is ended directly, and the current O does not need to be changed (because it’s connected to a O at the boundary).

Then continue to consider the next O, continue to do DFS.

Solution - Union Find

Union find data structure: https://en.wikipedia.org/wiki/Disjoint-set_data_structure

In computer science, union find is a tree-shaped data structure, used to deal with some disjoint sets merge and query problems. There is a union-find algorithm that defines two operations for this data structure:

• Find: Determine which subset the element belongs to. It can be used to determine whether two elements belong to the same subset.
• Union: Merging two sub-collections into the same set.

In order to define these methods more precisely, we need to define how to represent collections. A common strategy is to select a fixed element for each collection, called a representative, to represent the entire collection. Next, find(x) returns the representatives of the set to which x belongs, and union() uses the representatives of the two sets as parameters.

Knowing the union-find, it’s easy to find a solution to the problem. We can find that what we do is the problem of classification. In fact, O is ultimately divided into two categories, one can be connected to the boundary, and the other can not be connected to the boundary.

We need to iterate over each O node and merge it with the O nodes above, below, left and right.

If the current node is the boundary O, merge it with the dummy node (a node outside all nodes). Finally, all O nodes and dummy nodes connected to the boundary will be combined into one category. The other O nodes that are not connected to boundary O are another category.

Finally, we only need to find out whether each O node is the same as the dummy node.

public void solve(char[][] board) {
    int rowNum = board.length;
    if (rowNum < 3) {
        return;
    }

    int colNum = board[0].length;
    if (colNum < 3) {
        return;
    }

    // at least 3 * 3
    UnionFind unionFind = new UnionFind(rowNum * colNum + 1);

    // create a dummy node
    int dummyNode = rowNum * colNum;

    // first loop, connect border with dummy node
    // or connect all 'o' node
    for (int i = 0; i < rowNum; i++) {
        for (int j = 0; j < colNum; j++) {
            if (board[i][j] == 'O') {
                // border
                if (i == 0 || i == rowNum - 1 || j == 0 || j == colNum - 1) {
                    unionFind.union(dummyNode, i * colNum + j);
                } else {
                    // connect up, left, down, right
                    if (board[i - 1][j] == 'O') {
                        unionFind.union(i * colNum + j, (i - 1) * colNum + j);
                    }

                    if (board[i + 1][j] == 'O') {
                        unionFind.union(i * colNum + j, (i + 1) * colNum + j);
                    }

                    if (board[i][j - 1] == 'O') {
                        unionFind.union(i * colNum + j, i * colNum + (j - 1));
                    }

                    if (board[i][j + 1] == 'O') {
                        unionFind.union(i * colNum + j, i * colNum + (j + 1));
                    }
                }
            }
        }
    }

    // now that everything is classified into 2 classes
    // second loop to find all node not same as dummy node
    for (int i = 0; i < rowNum; i++) {
        for (int j = 0; j < colNum; j++) {
            if (unionFind.isConnected(i * colNum + j, dummyNode)) {
                board[i][j] = 'O';
            } else {
                board[i][j] = 'X';
            }
        }
    }
}

public class UnionFind {
    // each node point to it's parent, the parent of the root is itself
    private int[] parent;

    public UnionFind(int size) {
        parent = new int[size];

        for (int i = 0; i < size; i++) {
            parent[i] = i;
        }
    }

    // union 2 trees together, change root of node2 to node1
    public void union(int node1, int node2) {
        int root1 = findRoot(node1);
        int root2 = findRoot(node2);

        if (root1 != root2) {
            parent[root2] = root1;
        }
    }

    public boolean isConnected(int p, int q) {
        return findRoot(p) == findRoot(q);
    }

    // find the root of the node
    public int findRoot(int node) {
        // loop until find parent is itself
        while (parent[node] != node) {
            parent[node] = parent[parent[node]];
            node = parent[node];
        }

        return node;
    }
}