Leetcode 11: Container With Most Water

Question

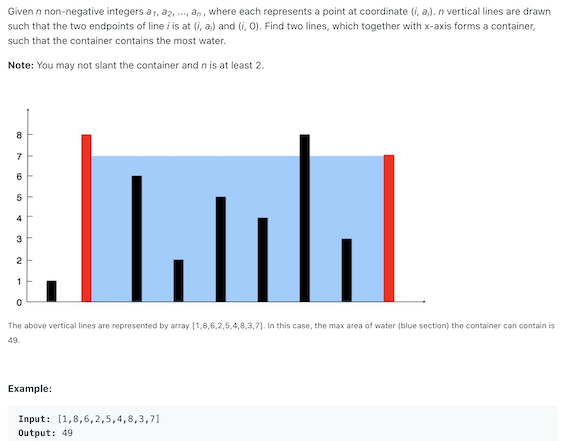
Each element of the array represents a height of a column. We want to pick 2 columns that can hold the most amount of water (shorter column height * distance between 2 columns).

Solution 1

The most naive method is brute force. Check each pair of elements and calculate the result. Use a variable to store the largest one. We need 2 for loops, so the time complexity is O(n²). The good thing is that no extra space required. Thus space complexity is O(1).

Solution 2

The amount of water is determined by shorter column height and distance between 2 columns. If we start from maximun distance (in the following example, index 0 and 8). Then the height is column 0 as we are getting the shorter column height.

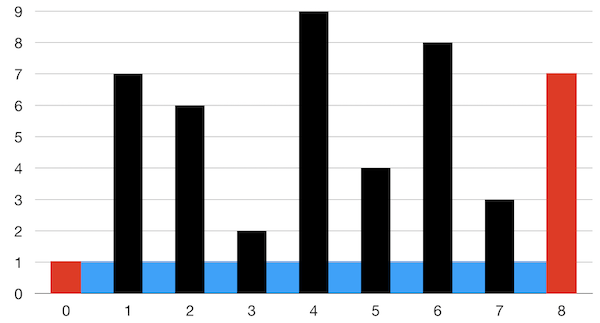
If we want to have a larger area, we can only reduce the distance and increase the height. So do we move the column 0 to column 1 ? Or column 8 to column 7? Of course, we will move the column that is shorter, so that the height might be increased.

In this example, if we change the column 8 to column 7, the distance is reduced, but the height is still unchanged (column 0 is still shorter), so the area will be reduced. But if we move column 0 to column 1, then column 8 becomes the shorter column and the area may increase.

What if 2 columns have the same height? Well, in this case it doesn’t matter which one we move. There will be 2 Circumstances.

There are 0 or 1 column between the 2 columns that is higher. Then the maximun area is when we choose these 2 same height column. As no matter how we move, the height is always less than these 2 columns, and distance is also smaller.
There are 2 or more columns between the 2 columns that is higher. These 2 columns will move to higher columns eventually, no matter which one moves first.

So the algorithm goes as follows:

Have 2 pointers. one at start of array and one at the end of array.
Each time move one pointer with smaller height inward
Use a variable to record the area each time
Loop until 2 pointers cross

Code

int result = 0;
int left = 0;
int right = height.length - 1;

while (left < right) {
    result = Math.max(result, (right - left) * Math.min(height[left], height[right]));

    if (height[left] < height[right]) {
        left++;
    } else {
        right--;
    }
}

return result;

We only loop the array once, so time complexity O(n). Space complexity O(1)

Question

Similar Questions

Solution 1

Solution 2